Introduction
Imagine a world without zero...Strange, right? We take zero for granted, believing it to be the foundation of our modern number system. But in 1947, mathematician James Foster introduced a system that functions identically to ours—except it lacks zero entirely. This alternative method challenges our perception of numbers and arithmetic, proving that while we may rely on zero, we don’t strictly need it. Let’s explore this fascinating concept and how it might change the way we think about mathematics.
Why Zero Matters—And What Happens Without It
In our familiar system, numbers follow a structured pattern: once we reach 10, we introduce a new place value, using zero to denote an absence of loose objects. For example:
- 30 represents three tens and zero additional units.
- 407 shows four hundreds, no tens, and seven units.
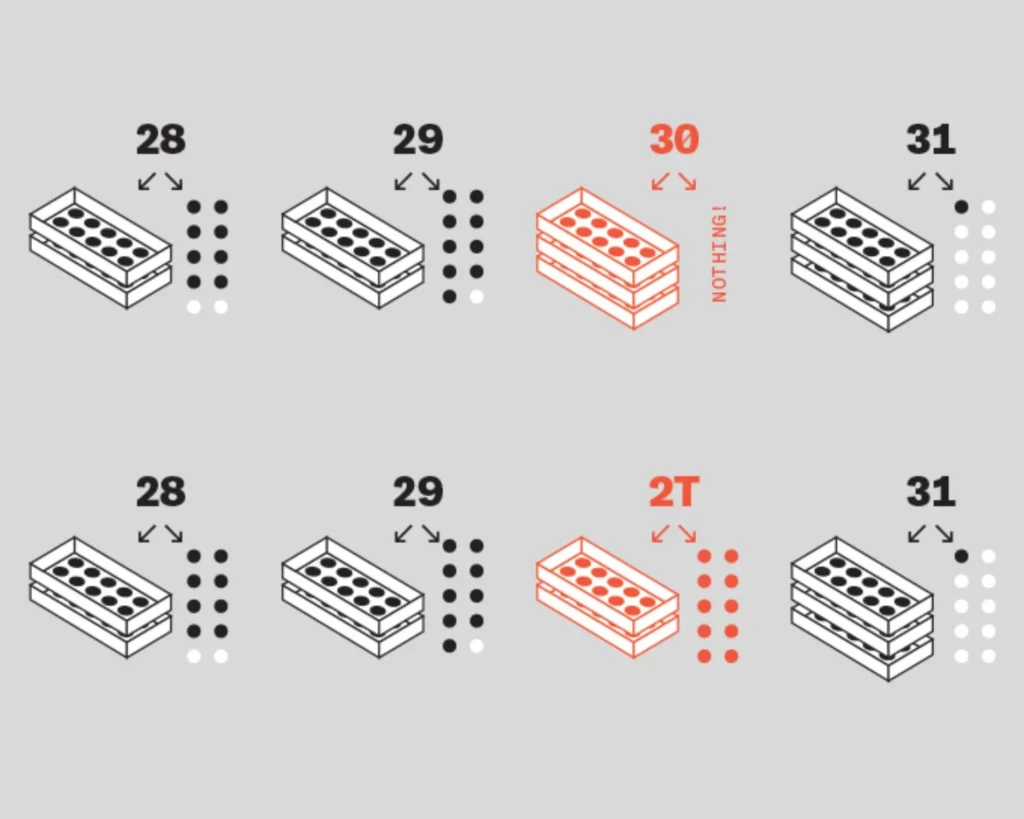
Foster’s system reimagines this approach. Instead of using zero, he proposed waiting before boxing numbers into new groups. In his system:
- 10 is written as T (ten loose objects).
- 30 becomes 2T (two boxed 10s) plus an unboxed 10.
- 106 turns into T6 (ten 10s and six ones).
- 3,090 appears as 2T8T (two thousand, ten hundred, and eighty-ten).
While this may seem unusual, the system remains logically sound, proving that zero—while convenient—isn’t strictly necessary.
The Strange Logic of a Zero-Free World
Foster’s system operates as an uncanny parallel to ours. Numbers that don’t contain zeros remain unchanged (e.g., 1,776 is still 1,776). However, any number traditionally requiring zero undergoes transformation. This raises some intriguing questions:
- What year would it be today? A year like 2024 might be written as 1T2T4 (one thousand ten hundred twenty-ten-four).
- How would salaries be affected? A six-figure income might not carry the same prestige if it’s written as 9T0 instead of 900,000.
- Would sports records look different? Wilt Chamberlain’s legendary 100-point game might instead be referred to as 9T points.
Everyday Life in a Zero-Free Society
A world without zero would force changes in multiple aspects of culture and technology:
- Anniversaries and Celebrations: Would cities commemorate a 111th anniversary instead of a 100th?
- Technology and Coding: Computer systems, built heavily around binary (which relies on zero), would require massive restructuring.
- Mileage Tracking: On car odometers, a rollover at “999,999” wouldn’t exist. Instead, we’d be eagerly watching for 9T9T9T9T!
Conclusion
Foster’s system may seem bizarre, but it highlights an important mathematical truth: we don’t need zero—we just prefer it. While his system is logically sound, our reliance on zero has shaped the way we think, calculate, and communicate. Spending even a short time in a world without zero makes us appreciate the simplicity it provides.
So, the next time you see a zero on your screen, remember—it’s nothing… but it means everything.


